Главная
12. Расчет ферм на подвижную нагрузку
Подвижной нагрузкой будем называть такую, как правило, вертикальную нагрузку, которая может перемещаться в пределах сооружения. Подобная нагрузка создается, например, движущимся по мосту транспортом или перемещающимися по подкрановым путям мостовыми кранами. При этом усилия, возникающие в сооружении, будут зависеть от положения нагрузки. Будем считать, что нагрузка перемещается по сооружению с небольшими ускорениями, поэтому динамическими эффектами, возникающими при этом можно пренебречь.
Задача расчета сооружений на подвижную нагрузку состоит в определении внутренних усилий в ее сечениях при любом ее положении. В частности, важно найти невыгоднейшее или опасное положение нагрузки, т.е. такое положение, при котором усилие в данном элементе конструкции достигает максимального по модулю значения. По усилиям, возникающим при невыгоднейшем положении груза, и выполняется подбор сечения стержней в системе.
Поскольку фермы часто используются в пролетных строениях мостов, в качестве несущих конструкций эскалаторов в метрополитенах, как стрелы подъемных кранов, их часто приходится расcчитывать на действие подвижной нагрузки.
Расчет стержневых систем на подвижную нагрузку выполняется при помощи линий влияния. Линия влияния внутреннего усилия в каком-либо сечении стержня - график зависимости этого усилия от положения единичной вертикальной силы на ездовой линии.
Рассмотрим вначале простую
балку на двух опорах, перекрывающую пролет L
(рис.12.1). Построим линии влияния реакции в левой опоре VA и
изгибающего момента MC в сечении в центре балки. Пусть единичная сила
приложена на расстоянии x от левой опоры. Из условия равенства нулю суммы проекций
всех действующих на систему сил на вертикальную ось
имеем VA =
1-VB.
Из условия равенства нулю суммы всех приложенных к системе моментов
относительно точки А
имеем 1
x = VB L. Отсюда следует, что 
. График данной зависимости и представляет
собой линию влияния опорной реакции VA (рис.12.1). При построении линий влияния ее
положительные ординаты принято откладывать вверх.
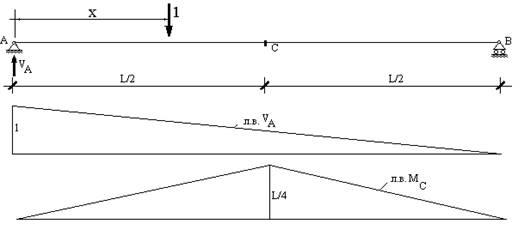
Рис.
12.1
Итак, при перемещении груза от левой опоры к правой величина опорной реакции VA уменьшается от единицы до нуля по линейному закону.
Для построения линии
влияния изгибающего момента Mc необходимо рассмотреть
два случая, когда груз находится левее и правее рассматриваемого сечения С. В первом случае 
выражение
для изгибающего момента имеет вид
Во
втором случае 
Соответственно, линия влияния Mc состоит из двух ветвей
(рис.12.1). Изгибающий момент в центре пролета балки равен нулю при нахождении
груза на опорах и достигает максимального значения, когда положение единичной
силы совпадает с рассматриваемым сечением (при 
).
Важно четко уяснить разницу между эпюрой и линией влияния. При построении эпюры определяются внутренние усилия в различных сечениях системы при неподвижной нагрузке, а при построении линии влияния определяется усилие в каком-то одном сечении при разных положениях единичной силы, действующей на систему.
В фермах нагрузка обычно передается на узлы посредством вспомогательных конструкций, например через настил и систему продольных и поперечных балок (рис.12.2). То есть, если единичная сила находится на ездовой линии и не над узлом фермы, то все равно имеет место узловая передача нагрузки, а значит в стержнях фермы не возникает никаких усилий, кроме продольных.
Рис. 12.2
Для построения линий влияния в стержнях ферм применяют те же приемы, что и при определении усилий в них от действия неподвижной нагрузки, в частности способ сечений. Необходимо только задаться координатой единичной силы на ездовой линии и проанализировать зависимость величины усилия в стержне от ее изменения.
В некоторых фермах со сложной решеткой, например шпренгельных, линии влияния могут иметь довольно сложный вид.
В раскосных фермах и фермах с треугольной решеткой ситуация несколько проще. Усилие в стержне при нахождении единичной силы слева от панели (рис.12.3), в которой находится этот стержень, будет меняться по одному закону, при нахождении справа от нее (рис. 12.4) - по другому закону, а при нахождении в пределах данной панели (рис. 12.5) - по третьему закону. В последнем случае необходимо учитывать, что часть от единичного усилия через вспомогательные конструкции передается на узел, лежащий на ездовой линии, слева от рассматриваемой панели, т.е. на часть фермы слева от сечения, а оставшаяся часть - на узел справа от рассматриваемой панели, т.е. с другой стороны от сечения. Таким образом, линии влияния продольного усилия в стержнях таких ферм в общем случае имеют три участка (рис. 12.6), причем часть линии влияния в пределах панели, которой принадлежит данный стержень, носит название передаточной прямой.
Рис.
12.3
Рис.
12.4
Рис.
12.5
Рис.
12.6
После того, как для стержня построена линия влияния, с ее помощью можно решить следующие задачи.
1. Пусть на ездовой линии находится
груз величиной Р. Тогда усилие в
стержне составит 
, где y
- ордината линии влияния под точкой приложения силы Р. Действительно, y - усилие,
возникающее в стержне от действия приложенной в данной точке единичной силы. В
силу линейности задачи, при увеличении нагрузки в Р раз, усилие в стержне тоже
возрастет во столько же раз.
На основании принципа независимости действия сил, если на ездовой линии имеется система из n сил, то усилие в стержне будет определяться по формуле:
где yi - ордината линии влияния под i-ой силой величиной Pi (рис.12.7). Таким образом, линии влияния могут быть использованы и для определения усилий в стержнях ферм и при действии неподвижной нагрузки. Это может быть удобно, если нужно выполнить большое число расчетов для различных комбинаций нагрузок, приложенных к ферме.
Рис. 12.7
2. Пусть на участке длиной L1 ездовой линии действует равномерно распределенная нагрузка интенсивностью q. Во избежание недоразумений подчеркнем, что здесь как и ранее, так и далее, считается, что нагрузка приложена к вспомогательным конструкциям, а с них - передается на узлы фермы. В этом случае усилие в стержне фермы определяется по формуле:
где
-
площадь, ограниченная линией влияния под зоной действия нагрузки q (рис.12.8). Действительно, выделим в
зоне действия нагрузки q участок
бесконечно малой длиной dx
(рис.12.8). Элементарная равнодействующая сила, действующая на ферму, с этого участка составляет 
, а усилие, возникающее от ее действия в стержне, в соответствии с формулой (1)
составит 
. Для того, чтобы
найти усилие в стержне от действия всей нагрузки, необходимо проинтегрировать dN по длине 
:
Очевидно, площадь в (4.4) необходимо определять с учетом знака. То есть, часть площади w снизу от горизонтальной оси учитывается со знаком “минус”.
Рис. 12.8
3. Пусть система грузов перемещается по ездовой линии, причем расстояния между грузами остаются постоянными. Такая ситуация имеет место, например, при движении поезда или мостового крана по пролетному строению моста или по подкрановым путям. Невыгоднейшее положение данной системы грузов возможно только при условии, что один из грузов находится над какой-либо вершиной линии влияния (рис.12.9). Подчеркнем, что это условие необходимое, но недостаточное. Иными словами, не при любом подобном положении нагрузки усилие в стержне имеет экстремальное значение.
Рис. 12.9
Например, для случая,
приведенного на рис. 12.9, усилие от системы грузов в соответствии с (1)
составляет 
. При сдвиге системы грузов
вправо на величину 
такую, что ни одна из сил, приложенных к
системе, не перейдет при этом через какую-либо вершину линии влияния и не
выйдет за пределы фермы, усилие в стержне АВ
составит:
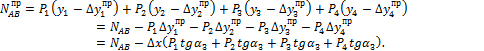
При сдвиге влево на ту же величину ∆x оно составит
Здесь 
и 
-
абсолютные значения изменения ординаты линии влияния под i-м грузом при сдвиге системы грузов вправо и влево соответственно,
- абсолютное значение угла наклона линии
влияния на i-м ее участке (рис.12.9).
Таким образом, изменение величины усилия в
стержне при сдвиге груза вправо составит 
, а при сдвиге влево 
. Очевидно, эти значения могут быть как
одного, так и разных знаков. Если 
и 
оказываются одного знака, то это значит, что
при сдвиге системы грузов как вправо, так и влево усилие в стержне либо
уменьшается, либо увеличивается, то есть оно имеет локальный экстремум.
В то же время, для случая когда ни один из
грузов не находится над вершиной линии влияния, величины
и могут
быть только разных знаков, а значит экстремум усилия в стержне в этом случае
невозможен.
Действительно, рассмотрим в качестве примера ситуацию, изображенную на рис.12.10. В этом случае при сдвиге вправо:
А при сдвиге влево:
Рис. 12.10
Сопоставляя выражения для и , можно сделать вывод, что они не могут быть
одного знака.
Итак, для поиска максимально и минимально возможных усилий в стержнях фермы при действии на нее подвижной системы грузов достаточно рассматривать только такие положения этой системы, при которых хотя бы один из грузов находится над какой-либо вершиной линии влияния.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
