Главная
13. Примеры расчета фермы на подвижную
нагрузку
Пример 1. Рассмотрим ферму, изображенную на рис. 13.1.
Необходимо:
1. Используя теорию линий влияния, определить усилие в стержне фермы 2-3 от действия неподвижной системы сил, изображенной на рис.10.1 (раздел 10).
2. Определить максимальное и минимальное усилия в стержне фермы 2-3 при движении по ездовой линии (по горизонтали от узла 1 к узлу 10) системы из двух сил (рис.13.1).
Рис. 13.1
3. Определить усилие от постоянной равномерно распределенной нагрузки q=10 кН/м, приложенной к поясу фермы, совпадающему с ездовой линией (рис. 13.2).
Рис. 13.2
Решение.
Построим линию влияния для стержня фермы 2-3. Для этого достаточно определить усилие в этом стержне при различных положениях единичной силы на ездовой линии.
Если единичная сила находится на расстоянии х от левой опоры, то реакция в последней
будет составлять 
, а в правой опоре - 
(рис.
13.3).
Рис. 13.3
Cоставим
уравнения равновесия узла 2 (рис. 13.4): 
откуда
следует, что 
. Поскольку, нагрузки к узлу 2 не приложены,
т.к. он не лежит на ездовой линии, это уравнение справедливо при любом
положении грузов на ней.
Рис. 13.4
Для определения 
воспользуемся способом сечений, причем
рассмотрим два случая, когда единичный груз находится слева от панели, в
которой располагается стержень 2-5 (рис. 13.5), и справа от нее (рис. 13.6).
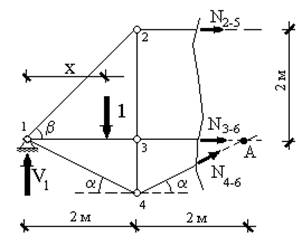
Рис. 13.5
Для первого случая (рис. 13.5) уравнения
равновесия моментов относительно точки А примет вид: 
откуда: 
. Следовательно, при нахождении единичного
груза слева от рассеченной панели (x<2м)
, а 
.
Согласно этой формуле, при x=0 ордината линии влияния, как и следовало ожидать, равна нулю, а при x=2 м она равна 1/2. По этим точкам строится левая ветвь линии влияния (до точки С на рис.13.7).
Для
второго случая (рис.13.6) из аналогичных рассуждений получим: 
, откуда: 
. Следовательно, при нахождении единичного
груза справа от рассеченной панели (x>4м)
, а 
. Таким образом, при x=4м ордината линии влияния равна 1 (точка D на рис.13.7), а на правой опоре, как и следовало ожидать - нулю.
По этим точкам строится правая ветвь линии влияния, и далее передаточная прямая
CD. В рассматриваемом случае ее
направление, как мы видим, совпадает с направлением левой ветви линии влияния,
а сама линия влияния оказалась симметричной.
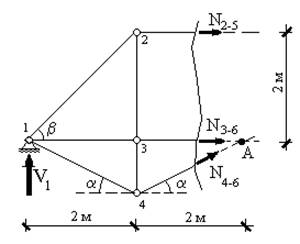
Рис.13.6
Теперь приступим к определению усилий в стержне 2-3.
Для заданной неподвижной
узловой нагрузки (рис.10.1, раздел 10) в соответствии с формулой (1, раздел 12)
найдем величину усилия в стержне: 
. Этот же ответ был получен
нами ранее в разделе “Пример расчета фермы на неподвижную нагрузку” без
использования линий влияния, что подтверждает правильность проделанных
вычислений.
Рис. 13.7
Наиневыгоднейшим
положением подвижной системы двух сил на ездовой линии (рис.13.1) будет
положение, когда одна из них находится ровно посередине пролета фермы
(рис.13.8), т.к. в этом случае одна из сил оказывается над единственной в
рассматриваемом случае вершиной линии влияния. Ордината линии влияния под силой
в центре фермы равна 1, ординату под точкой приложения второй силы легко
определить из подобия треугольников: 
, откуда y=0,8
(рис.13.8). В соответствии с (1, раздел 12) усилие в стержне составит 
. В силу симметрии линии влияния, в случае,
когда над ее вершиной в центре пролета фермы окажется не левая, а правая сила,
результат будет тем же.
Построенная линия влияния не имеет отрицательных ординат, следовательно, при любом положении системы сил на ездовой линии в стержне будут возникать только растягивающие усилия. Поэтому, максимальным возможным усилием в стержне 2-3 для рассматриваемой подвижной нагрузки является 36 кН, минимальным -0 кН.
Рис. 13.8
Наконец, определим усилие в стержне от
действия неподвижной равномерно распределенной по всей длине ездовой линии
нагрузки (рис.13.2) q=10 кН/м.
Площадь фигуры, ограниченной линией влияния (рис.13.7) составляет 
. Размерность площади фигуры оказалась такой,
поскольку единичная сила, а следовательно и ординаты
линии влияния продольного усилия не имеют размерности.
Теперь, в соответствии с формулой (2, раздел
12), определим усилие в стержне: 
.
Пример 2. Для фермы, показанной на рис. 13.9, а требуется:
1) определить
(аналитически) усилия в стержнях третьей панели;
2) построить линии
влияния усилий в тех же стержнях;
3) по линиям влияния
подсчитать значения усилий от заданной нагрузки и сравнить их со значениями,
полученными аналитически.
Решение.
1. Определяем усилия
в стержнях фермы
Расчет начинаем с
определения опорных реакций. Поскольку ферма и нагрузка симметричны, 
.
Для определения
усилий в стержнях фермы применяем метод сечений. Желательно так вести
вычисления, чтобы усилие в каждом стержне определялось независимо от усилий в других
стержнях. Это избавляет от нарастания погрешности расчета и увеличивает его
точность. Для этого надлежит придерживаться следующего порядка:
а) провести разрез
фермы, который должен проходить не больше чем через три стержня, в том числе и
через стержень, усилие в котором требуется определить.
б) отбросить левую
или правую часть фермы (удобнее отбрасывать наиболее нагруженную часть фермы).
в) заменить
действие отброшенной части фермы неизвестными усилиями в разрезанных стержнях;
при этом усилия всегда следует направлять от разреза, предполагая их
растягивающими (положительными);
г) составить такое
уравнение статики, чтобы, по возможности, только искомое усилие входило в него
как неизвестное.
д) решить уравнение
и найти это усилие; если результат будет со знаком плюс, то стержень растянут;
если со знаком минус, то стержень сжат.
Усилие 
(нижний пояс). Проведем разрез n-n и отбросим
правую часть фермы (рис. 13.9, б).
Для того чтобы в уравнение для не вошли усилия 
и 
, следует записать
сумму моментов всех сил, приложенных к оставшейся части фермы, относительно
узла 5, в котором пересекаются линии действия этих усилий. Такая точка
называется моментной. Эта точка всегда находится на пересечении линии действия
усилий в двух других стержнях, попавших в разрез:
Отсюда 
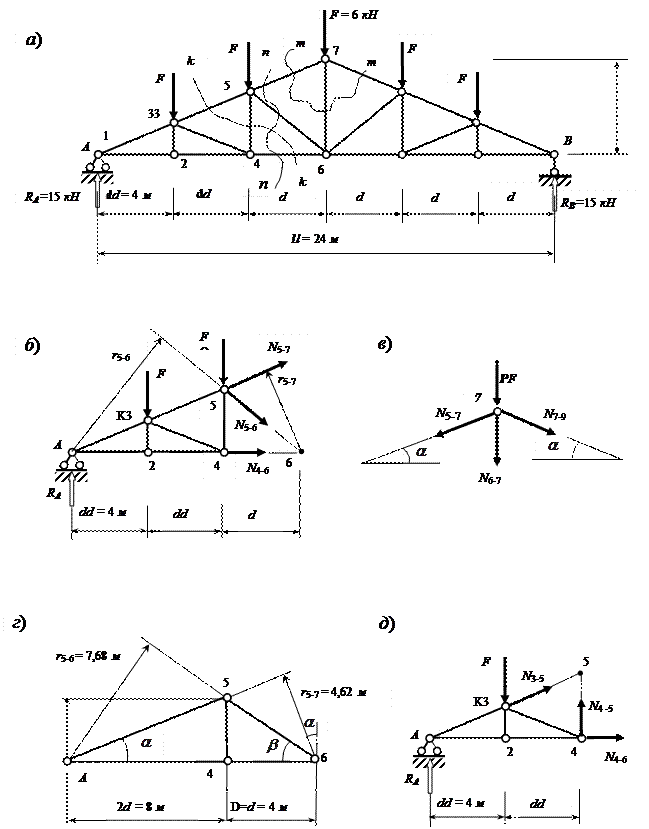
Рис. 13.9.
Определение усилий в стержнях простой фермы:
а –
расчетная схема фермы; б – разрез n–n; в – разрез m–m; г –
к определению плеч усилий; д – разрез
k–k
Усилие (верхний пояс). Для нахождения воспользуемся тем же разрезом n-n (рис. 13.9, б), но
теперь моментная точка будет на пересечении линий действия и в узле 6:
Откуда
Усилие (раскос). Для определения вновь воспользуемся разрезом n-n (рис. 13.9, б). Моментная точка находится
на пересечении линий действия усилий и в узле А. Проводя из этого узла перпендикуляр на линию действия искомого
усилия (рис. 13.9, г), получим плечо усилия относительно узла 1.
Тогда
Усилие 
(правая стойка). Для нахождения воспользуемся разрезом m-m (рис. 13.9, в).
Рассмотрим равновесие узла 7.
следовательно 
;
Откуда
Усилие 
(левая стойка). Для нахождения воспользуемся разрезом k-k (рис. 13.9, д). Теперь моментная точка будет на
пересечении линий действия усилий 
и в узле А, а плечо
усилия относительно узла А равно 2d.
, откуда 
2. Построение линий влияния
2.1. Линии влияния опорных реакций
Линии влияния опорных реакций в балочной
ферме (рис. 13.10, а)
определяются так же, как для однопролетной балки. Поэтому линии влияния этих
реакций не отличаются от линий влияния опорных реакций балок (рис. 13.11, б, в).
Рис. 13.11. Построение
линий влияния усилий в простой ферме
2.2. Линия влияния усилия
Воспользуемся
разрезом n-n (рис. 13.10, а). Рассмотрим два положения единичного груза:
справа и слева от разрезанной панели. При положении груза 
справа от разреза рассматриваем равновесие
левой отсеченной части фермы (рис. 13.10, в) и составляем сумму моментов
относительно моментной точки – узла 5:
Откуда 
т. е. правый
участок 
отличается от 
лишь
постоянным множителем 2,4.
Строим правую
прямую линии влияния 
, откладывая на левой
опорной вертикали ординату 2,4 и соединяя ее с нулевой точкой на правой опорной
вертикали (рис. 13.11, г). Полученную
правую прямую используем на участке движения груза справа от разрезанной
панели.
При положении груза
слева от сечения n–n составляем условие равновесие правой отсеченной части
фермы (рис. 13.10, б):
Откуда
т. е. левый участок
имеет такой же вид, как 
. Умножая ординаты на множитель
4,8, получаем левую прямую (рис. 13.11, г).
При
положении груза в пределах разрезанной панели линией влияния
будет передаточная прямая, соединяющая крайние ординаты (передаточные прямые на
рис. 3 показаны жирными линиями).
2.3. Линия влияния усилия
Вновь
воспользуемся разрезом n-n (рис. 13.10, а). Рассмотрим два
положения единичного груза: справа и слева от разрезанной панели. При
нахождении груза справа от разреза
рассматриваем
равновесие левой отсеченной части фермы (рис. 13.10, в) и составляем
сумму моментов относительно моментной точки – узла 6:
Откуда 
т. е. правый участок 
отличается от . лишь постоянным множителем 2.6 и знаком минус. Все ординаты изменяются в 2,6 раз и откладываются от оси в
отрицательном направлении, т. е. вниз (рис. 13.11, д). Построенную таким образом правую прямую используем на
участке движения груза справа от разрезанной панели.
При
положении груза слева от разрезанной панели составляем условие равновесия
правой отсеченной части (рис. 13.10, б):
Откуда
т.
е. левый участок отличается от лишь постоянным
множителем 2,6 и знаком минус. Все ординаты изменяются в 2,6 раз и откладываются от оси в
отрицательном направлении т.е. вниз (рис. 3, д). Полученную левую прямую используем на участке движения груза
слева от разрезанной панели. В пределах
разрезанной панели соединяем крайние ординаты прямой линией.
Отметим, что в
рассмотренных линиях влияния правая и левая ветви линии влияния пересеклись под
моментными точками. Это не случайно и вытекает из их построения. Эту
зависимость будем использовать в дальнейшем для проверки правильности
построения линий влияния.
2.4. Линия влияния усилия
Воспользуемся
разрезом n-n (рис. 13.10, а). При положении груза справа от разреза рассматриваем равновесие
левой отсеченной части фермы (рис. 13.10, в)
и составляем сумму моментов относительно моментной точки – узла 1:
Откуда
, т. е. при грузе , расположенном
справа от разреза, усилие равно нулю. Правая прямая линии влияния в этом
случае сливается с осью линии влияния (рис. 13.11, е).
Для
построения левой прямой линии влияния рассмотрим условие равновесия правой
отсеченной части фермы (рис.13.10, б):
Откуда
Это означает, что
усилие равно опорной реакции RB, умноженной на (–3,125).
Для построения
графика этой зависимости откладываем на правой опорной вертикали вниз отрезок
3,125 и соединяем его конец с нулевой точкой на левой опорной вертикали. В
пределах разрезанной панели соединяем крайние точки левой и правой ветвей
передаточной прямой. Построенная таким образом линия влияния изображена на рис. 13.11, е. Отметим, что вновь правая и левая ветви линии влияния
пересеклись под моментной точкой – узлом 1.
2.5. Линия влияния усилия
Вырежем узел 7 (рис. 13.10, е) и спроектируем действующие на этот узел силы на
горизонтальную ось:
следовательно, .
Спроектируем те же силы
на вертикальную ось:
откуда 
.
Таким образом,
линия влияния может быть получена умножением всех ординат
линии влияния на
коэффициент (-2∙sinα). Линия влияния имеет вид
треугольника (рис. 13.11, ж) с наибольшей
ординатой (под узлом 7), равной
1,300(2∙0,3846)=1,000.
Если же груз перемещается по верхнему поясу фермы («езда
поверху»), то в тот момент, когда он окажется в узле 7, уравнение 
примет вид
откуда 
Следовательно, в
этом случае ордината на линии влияния под узлом 7 меньше на единицу, чем ордината на
этой же линии влияния при езде по нижнему поясу, и равна нулю (сплошная линия
на рис. 13.11, ж).
2.6. Вычисление по
линиям влияния усилия от заданной постоянной нагрузки
При вычислении
усилий в стержнях от сосредоточенных сил P=6 кН уравнение (1, раздел 12) принимает более простой вид
Тогда
Найденные с помощью
линий влияния усилия в стержнях фермы совпадают с полученными аналитически
значениями.
Пример
3. В стержнях фермы, как мы знаем, возникают только нормальные
силы – сжимающие или растягивающие. Рассмотрим, как стоятся
линии влияния усилий в стержнях фермы (рис.13.12). В качестве метода у нас все
тот же метод сечений, а в качестве «инструмента» исследований – уравнения
равновесия. Другими словами, покажу, как рассмотренные ранее аналитические
способы определения усилий в стержнях фермы применяются для построения линий
влияния этих усилий.
Следует различать, по какому поясу
перемещается единичная сила. Если проекции узлов совпадают, то это не
принципиально, но когда проекции узлов не совпадают, то вид линий влияния при
езде по верхнему поясу и нижнему будут различны.
По аналогии с балкой рассмотрим два возможных положения единичной силы – слева и справа от рассеченной панели или в узле и вне узла и, опять же, рассеченной панели.
Рис.13.12
Решение.
Традиционно начнем с линий влияния опорных
реакций. Не трудно убедиться, что они имеют тот же вид, что и для аналогичной
балки, т.е. балки того же пролета и схемы опирания
(см. рис. 13.12).
Линия влияния SA-1.
Применим способ вырезания узлов. При этом
учтем, что единичная сила не может находиться на рассеченной панели.
Вырежем узел А (см. рис. 13.12) и рассмотрим
два возможных положения единичной силы:
1. F=1 вне вырезанного узла, т.е. в узле 1 или справа от него.
Рассмотрим условие равновесия узла А
Полученный закон изменения л.в. SA-1 справедлив там, где расположена
единичная сила, т.е. от узла 1 вправо. Построим
соответствующую ветвь линии влияния с учетом того, что л.в.
VA нам известна.
Другими словами, следует построить л.в. VA и ординаты ее уменьшить на sin𝛼
.
2. F=1 в вырезанном узле, т.е. в узле А.
Запишем условие равновесия узла А
Когда единичная сила находится в узле А, то опорная реакция VA равна ей, тогда
SA-1=0.
Получили конкретное значение величины
ординаты л.в. SA-1. В пределах рассеченной панели имеющие два значения л.в. SA-1
(слева и справа) соединим передаточной прямой (см. рис. 13.12).
Из подобия треугольников по имеющемся значению ординаты легко вычисляются ординаты под
узлами фермы – понадобятся для определения усилия по л.в.
и заданной постоянной нагрузке.
Аналогично построена линия влияния SA-2,
только закон ее устанавливается через л.в. SA-1.
Проделайте построение самостоятельно и сравните с приведенным
на рис. 13.12.
Линия
влияния S1-3.
Для построения л.в. S1-3 воспользуемся способом моментной точки, которой для него является узел 4.
1. F=1 справа от рассеченной панели (рис. 13.12).
Рассмотрим равновесие левой отсеченной части,
т.е. той, к которой приложено меньшее число воздействий:
Обратим внимание на то, что
произведение 
, так как VA представляет собой линию влияния, является л.в. изгибающего момента в балке в сечении 4. Тогда
2. F=1 справа от рассеченной панели.
Рассмотрим равновесие левой отсеченной части:
Откуда
Объединив два случая, получим, что при любом положении единичной силы по отношению к рассеченной панели, линия влияния S1-3 будет определяться выражением:
Л.в. S1-3 показана на рис. 13.12.
Полученный результат можно обобщить и на
другие случаи применения способа моментной точки при построении линий влияния,
если:
– проекции узлов верхнего и нижнего поясов
фермы совпадают;
– моментная точка находится в пределах
пролета фермы, но не на опорах.
Аналогично построены
л.в. S2-4, S3-5 (рис. 13.12). Выполните построения
самостоятельно.
Линия
влияния S4-5 (рис. 13.12).
Применим способ проекций.
1. F=1 справа от рассеченной панели.
Откуда
Правая ветвь л.в. S4-5 (до рассеченной панели) представляет л.в. VA, ординаты которой уменьшены в sin β раз.
2. F=1 слева от рассеченной панели.
откуда
Левая ветвь л.в. S4-5 (до
рассеченной панели) представляет л.в. VВ, ординаты которой уменьшены
в sin β
раз.
В пределах рассеченной панели две известные
ординаты – в узлах 3 и 5, соединим передаточной прямой.
Если
при построении линий влияния были приняты положительные направления усилий
(растянуты), то полученные знаки в аналитических выражениях переносятся на сами
линии влияния, не забывайте только на какую ветвь.
Линии влияния усилий в стержнях фермы с
успехом можно использовать для определения усилия от заданной нагрузки по
формуле
Пример 4. Рассмотрим ферму (рис. 13.13,а). При воздействии только вертикальной нагрузки ее опорные реакции будут такими же как у вспомогательной балки (рис. 13.13,б). Поэтому л.в. опорных реакций фермы будут аналогичны л.в. балки (рис. 13.13,в, г).
Решение.
Для построения л.в. продольных
усилий фермы воспользуемся способами вырезания узлов и сквозных сечений.
а) Использование способа вырезания узлов
Для построения л.в. N2-6
вначале рассмотрим узел 1. Так как к этому узлу силы не приложены, то по
признаку 1 N1-6=0.
После этого вырежем узел
6 фермы. Здесь могут быть два случая:
1) когда единичная сила P=1 находится в этом узле (рис. 13.13,е), то
ΣY= N2-6 sinα + 1 – 1=0.
Отсюда N2-6=0.
2) когда единичная сила P=1 находится вне этого узла (рис. 13.13,ж), то
ΣY=N2-6 sinα + RA=0.
Отсюда
Тогда, используя л.в. опорной реакции RA, можно построить л.в.
усилия N2-6
(рис. 13.13,д).
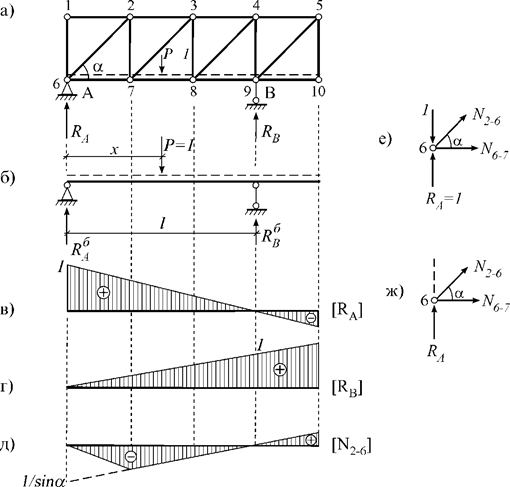
Рис. 13.13
б) Использование
способа сквозных сечений
Поперек фермы проведем сквозное
сечение I–I (рис. 13.14,а) и получим
независимые левые и правые части. Единичная сила P=1 может находиться в обоих частях фермы.
1) Единичная сила левее сечения
(рис. 13.14,б):
Отсюда
Отсюда
2) Единичная сила правее сечения (рис. 13.14,в):
Отсюда
Отсюда
В первом случае определяем ординаты л.в. этих усилий между
узлами 6-7, т.е. определяем их левые ветви, а во втором случае определяем ординаты
обоих л.в. между
узлами 8-10, т.е. определяем правые ветви л.в. Соединив точки между узлами 7-8, получаем переходную
прямую и окончательный вид л.в. (рис. 13.14,г,
д).
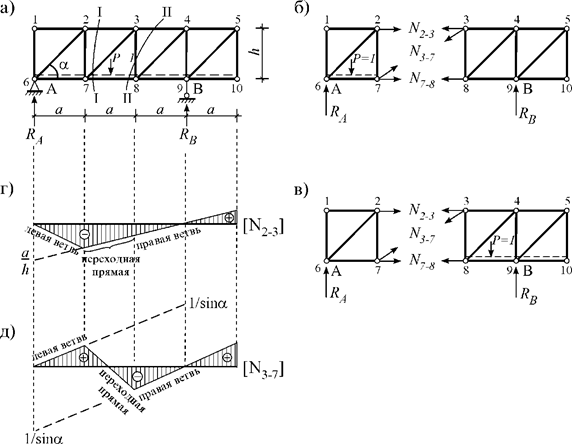
Рис. 13.14
Как видно из этих
примеров, у л.в. продольных усилий фермы есть
следующее свойства: ветви л.в. пересекаются под
моментной точкой; если же моментной точки нет, ветви л.в. параллельны.
Пример
5. Рассмотрим ферму (рис. 13.15,а). Построим л.в.
для усилий стержней 2-ой панели, а именно: N2-9;
N9-8; N2-8; N2-3 и N3-8.
Решение.
Линии влияния
опорных реакций строим по аналогии с л.в. реакций
простой балки (рис. 13.15,б,в). Груз Р = 1 движется по
верхнему поясу.
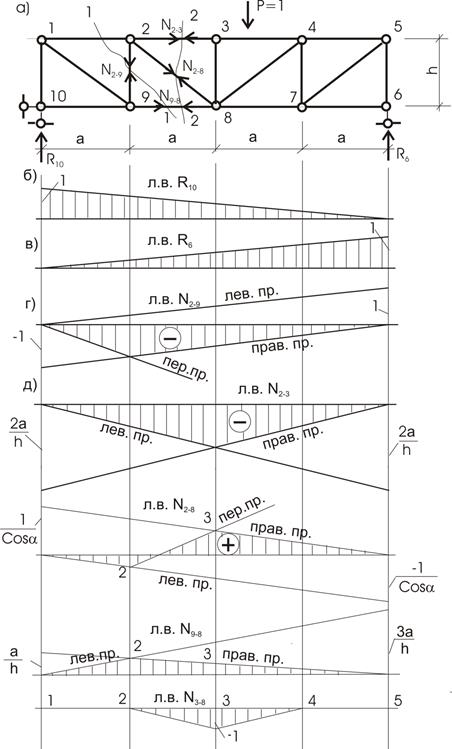
Рис.13.15
Линия влияния
N2-9 (рис. 13.15,г).
Наметим путь
определения усилия N2-9. Проведем
сечение 1 – 1, разрезав и стержень 2-9. Относительно этого сечения груз Р = 1 будет находиться слева и справа от
сечения 1-1.
1) Р = 1 слева от сечения 1 – 1 (на рисунке
груз не показан).
Рассматривая
правую незагруженную часть фермы, находим, используя одно из уравнений статики,
усилие N2-9:
или
л.в. N2-9= л.в. R6 (левая
прямая).
Левая прямая справедлива при грузе в 1 узле.
2) Р = 1 справа от сечения 1 – 1 (правая
прямая)
Рассмотрим
левую часть фермы – незагруженную
л.в. N2-9= - л.в. R10
Правая прямая справедлива от узла 2 до 5. От узла 1 левой прямой до 2 узла правой прямой проводим передаточную
прямую (рис. 13.15,г).
Линия
влияния N2-3 (рис. 13.15,д).
Воспользуемся сечением 2-2 и при нахождении N2-3 будем
пользоваться суммой моментов относительно узла 8.
а) Груз Р = 1 слева. Рассматриваем равновесие
правой части:
Отсюда
Линию влияния R6 увеличиваем в
раз (рис. 13.15,д). Левая прямая справедлива от узла 1 до
узла 2.
б) Груз Р = 1 справа (правая прямая).
Рассматриваем
равновесие левой части:
или
Правая прямая (рис.13.15,д)
справедлива от узла 3 до узла 5.
От узла 2 левой прямой до узла 3 правой прямой проходит передаточная
прямая, в данном случае совпадающая с левой прямой.
Линия
влияния N2-8 (рис. 13.15,е).
Используем
сечение 2- 2. В качестве исходного уравнения примем сумму проекций на ось «y».
а) Груз Р = 1 слева (рис. 13.15,е)
Отсюда
График
справедлив только от узла 1 до узла 2.
б) Груз Р = 1 справа от сечения (рис.13.15,е).
Отсюда
Правая прямая л.в. N2-8 будет
справедлива от узла 3 до узла 5.
От узла 2 левой прямой до узла 3 правой прямой займет место
передаточная прямая. Отметим особенность: для раскосов передаточная прямая
занимает положение, близкое к перпендикуляру к данному раскосу.
Линия
влияния N9-8 (рис. 13.15,ж).
Для этого
усилия основным уравнением примем 
а) Р = 1 слева (левая прямая)
Отсюда
б) Р = 1
справа (правая прямая)
Отсюда
Линия
влияния N3-8 (рис. 13.15,з)
Для
определения данного усилия воспользуемся вырезанием узла 3. Расположение
стержней, сходящихся в узел 3, попадает под частный случай.
Если в узел
сходятся три стержня, два из которых лежат на одной прямой, то, при отсутствии
нагрузки в этом узле, усилие в отдельно
стоящем стержне (N3-8) равно нулю.
Следовательно, если сила будет находиться в узлах 1, 2, 4, 5, усилие N3-8 = 0.
Если узел 3
будет загружен силой Р = 1, то N3-8 = -1.
От узла 2 до
узла 8 и от узла 3 до узла 4 на л.в. N3-8 будут занимать место передаточные
прямые (рис. 13.15,з).
13.1 Примеры расчета шпренгельной фермы на
подвижную нагрузку
Шпренгельные фермы характеризуются тем, что в
состав каждой панели простой фермы вводятся дополнительные двухопорные
фермочки -
шпренгели, работающие на местную нагрузку и передающие ее на узлы основной
решетки. Следует заметить, что шпренгели бывают двух видов - одноярусные и двухъярусные. Одноярусные шпренгели
передают нагрузку на тот же пояс, на котором они ее воспринимают. Двухъярусные
шпренгели воспринимают нагрузку на одном поясе, а передают ее на другой пояс
фермы. В шпренгельных фермах различают 4 основные группы стержней:
1) стержни, принадлежащие только основной решетке – усилия в этих стержнях определяются из рассмотрения основной фермы;
2) стержни, относящиеся только к шпренгелям – усилия в этих стержнях определяются из рассмотрения отдельных шпренгелей как самостоятельных ферм;
3) стержни, принадлежащие одновременно и основной решетке и шпренгелю: усилия в этих стержнях определяются как сумма усилий в соответствующем стержне основной фермы и слившемся с ним стержне шпренгеля; часто усилие в таком стержне может быть определено сразу из рассмотрения равновесия отсеченной части шпренгельной фермы (без ее разложения);
4) для ферм с двухъярусными шпренгелями
следует отдельно выделить еще стойки, на которые передают нагрузки двухъярусные
шпренгели; при определении усилий в таких стойках при рассмотрении основной
решетки фермы необходимо учитывать передачу нагрузки с одного пояса на другой.
Построение линий влияния усилий в стержнях
ферм обычно выполняется статическим
методом. При этом, проводя в ферме сечения, следует различать:
- панель
фермы – область между двумя соседними узлами на одном из поясов фермы;
- рассеченная
панель фермы (р.п.) – панель фермы, через которую
проведено сечение;
- расчетная
рассеченная панель фермы (р.р.п.) – рассеченная
панель того пояса (верхнего, нижнего), по которому движется груз;
При использовании для определения усилия
способов моментной точки или проекций ферма рассекается сечением на две части и
при построении л.в. нужно рассматривать три случая –
груз слева от р.р.п.; груз справа от р.р.п.; груз на участке р.р.п.
Сначала груз Р = 1 располагается с одной стороны от р.р.п. и из рассмотрения равновесия одной из частей фермы
(любой; более удобной с точки зрения расчета) определяется искомое усилие
(функция его изменения при движении груза) и строится соответствующая ветвь
линии влияния; затем груз Р = 1 располагается с другой стороны от р.р.п. и аналогично находится функция изменения л.в. искомого усилия и строится другая ветвь линии влияния.
На участках же р.р.п. проводится переходная
прямая. При использовании способа вырезания узлов следует рассматривать
следующие три случая – груз в узле; груз вне узла и вне р.р.п.;
и груз на участках р.р.п. (соседних с вырезанным
узлом).
При построении линий
влияния усилий в стойках ферм с двухъярусными шпренгелями необходимо,
рассматривая основную решетку, построить два варианта линии влияния усилия - при
движении груза по верхнему и по нижнему поясам; затем, последовательно
передвигая груз по всем узлам грузового пояса фермы, необходимо определить, на
какой из поясов груз передается и соответственно какая из линий влияния
реализуется.
С помощью линий влияния могут быть определены усилия в стержнях фермы от произвольной постоянной нагрузки точно так же, как и в балках. При этом усилия в одних и тех же стержнях, найденные из аналитического расчета ферм и по линиям влияния, должны, естественно, совпадать.
Пример 6. Для шпренгельной фермы (рис. 13.16) от заданной постоянной нагрузки требуется аналитически определить усилия в шести указанных стержнях, построить линии влияния этих усилий, определить их величины по линиям влияния и сравнить их с определенными из аналитического расчета фермы.
Рис.
13.16
Решение.
1. Аналитическое определение усилий от
заданной нагрузки.
Опорные реакции:
Проверка
опорных реакций:
Усилия в стержнях 2-3, 1-5, 1-6 можно найти из рассмотрения полной схемы шпренгельной фермы, проведя сечение I - I и рассматривая равновесие, например, левой отсеченной части фермы. При этом равномерно распределенную нагрузку, действующую на рассеченную панель, с учетом узловой передачи нагрузок необходимо распределить на соседние узлы; узловые нагрузки на узлы 2 и 3 при этом определяются через опорные реакции передаточной балочки пролетом 0,5d=0,75 м (Pq=0,5∙q∙0,5d=0,5∙4∙0,75=1,5 кН). В результате левая отсеченная относительно сечения I - I часть фермы будет иметь вид, показанный на рис. 13.17,б.
Рис.
13.17
Определяем
усилия в стержнях, попавших в сечение I - I:
S2-3 - ?
(способ моментной точки; моментная точка – в узле 1):
Σ
=0; 24∙1,5 - 4∙3-12∙0,75
+ S2-3∙0,9494∙1,5=0; S2-3=
-10,54 кН;
S1-5 - ?
(способ моментной точки; моментная точка – K):
Σ
=0; -24∙3 + 4∙1,5 +
12∙3,75 + 1,5∙4,5 - S1-5∙0,8∙4,5=0; S1-5=
-3,96 кН;
S1-6 - ?
(способ моментной точки; моментная точка – в узле 4):
Σ
=0;
24∙3 - 4∙4,5 - 12∙2,25 - 1,5∙1,5 - S1-6∙2=0; S1-6= 12,375 кН.
Усилие в стержне 3-5, относящемся к
шпренгелю, легко найти из вырезания узла 3 всей фермы (рис. 13.17,а):
ΣZ=0;
3cosα – S3-5∙cosα=0; S3-5= -3 кН;
ΣX=0; -S2-3cosα – S3-4∙cosα=0; S3-4=S2-3=
-23,18 кН.
Стержень 5-4 относится к основной ферме (1-ая группа) и усилие в нем можно найти из рассмотрения основной фермы (без шпренгелей) - см. рис. 13.18, проведя в ней сечение II - II и рассматривая левую отсеченную часть. При этом следует учесть, что нагрузки, воспринимаемые шпренгелями (см. рис. 13.18,б), необходимо передать на основную ферму в узлах их передачи от шпренгелей (см. рис. 13.18,а).
Рис.
13.18
В результате получим:
S5-4 -
? (способ моментной точки; моментная точка – K):
Σ=0; -24∙3 + 4∙1,5 + 6∙3 + 1,5∙4,5 + 7,5∙4,5 - S5-4∙0,8∙4,5=0; S5-4=
-2,08 кН.
Усилие в стойке 1-2 также можно найти из
рассмотрения основной фермы с учетом распределения нагрузок от шпренгелей на
узлы основной решетки. Проведем сечение III - III (см. рис. 13.18,а)
и рассмотрим левую отсеченную часть, используя способ моментной точки - точка К:
Σ=0; -(24 +6)∙3 + 4∙1,5
+ 1,5∙4,5 + S1-2∙4,5=0; S1-5=
-2,08 кН.
2. Строим линии влияния (л.в.) усилий в тех же стержнях
фермы (груз движется по верхнему поясу) – см. рис. 13.19.
Вначале
строятся линии влияния опорных реакций; делается это также,
как и для любой балочной системы (рис. 13.19).
Рис. 13.19
Линию влияния усилия в стержне 2-3 строим,
проведя сечение I - I (расчетная рассеченная панель 2-3), способом моментной точки - точка 1:
а) груз Р = 1 слева от расчетной рассеченной
панели (р.р.п.) - рассматриваем правую часть:
Σ
=0; -RB∙4,5 – S2-3∙cosα∙1,75 + S2-3∙sinα∙0,75 =0; S2-3=
-3,16∙RB;
л.в.S2-3 = (л.в.RB)∙(-3,16);
т.е. левую часть л.в.
S2-3
получим умножением всех ординат соответствующей части л.в.
RB на 3,16 и изменив знак на противоположный;
б)
груз Р = 1 справа от р.р.п.
- рассматриваем левую часть
фермы:
Σ=0; RA∙1,5 + S2-3∙0,949∙1,5
=0; S2-3= -1,054∙RA;
л.в.S2-3 = (л.в.RA)∙(-1,054);
аналогично правую часть л.в.
S2-3 получим
умножением всех ординат соответствующей части л.в. RA на 1,054 и изменив знак на противоположный;
в)
на участке р.р.п. проводим соединительную
прямую.
Линия
влияния S1-5 - ? (сечение I – I, способ моментной точки; моментная точка – K):
а)
груз Р = 1
слева от р.р.п. -
рассматриваем правую часть:
Σ
=0; -RB∙9 + S1-5∙0,8∙5,25
- S1-5∙0,6∙1 =0; S1-5=
2,5∙RB;
л.в.S1-5 = (л.в.RB)∙2,5;
б)
груз Р = 1
справа от р.р.п. -
рассматриваем левую часть фермы:
Σ=0; -RA∙3 - S1-5∙0,8∙4,5
=0; S1-5= -0,8333∙RA;
л.в.S1-5 = (л.в.RA)∙(-0,8333);
в)
на участке р.р.п. проводим соединительную
(переходную) прямую.
Линия
влияния S5-4 - ? (сечение II – II, для основной фермы; способ моментной точки, моментная точка –
K):
Несложно увидеть, что процедура построения л.в. S5-4 точно такая же, как и для л.в.
S1-5;
разница связана с тем, что для S5-4 р.р.п.будет
длиннее - между узлами 2 и 4,
поэтому и переходная прямая проходит на этом участке.
Л. в. S5-4 и S1-5 на рис. 13.19 совмещены.
Линия
влияния S1-6 - ? (сечение I – I, способ моментной точки; моментная точка – 4):
а)
груз Р = 1
слева от р.р.п. -
рассматриваем правую часть:
Σ
=0; S1-6∙2
- RB∙3 =0; S1-6=
1,5∙RB;
л.в.S1-6 = (л.в.RB)∙1,5;
б)
груз Р = 1
справа от р.р.п. -
рассматриваем левую часть фермы:
Σ=0; -S1-6∙2
+ RA∙3 =0; S1-6=
1,5∙RA;
л.в.S1-6 = (л.в.RA)∙1,5;
в) на участке р.р.п. проводим соединительную (переходную) прямую.
Линия
влияния S1-2 - ? (сечение III –
III, способ моментной точки; моментная
точка – K):
Для построения л.в. усилия в этой стойке шпренгельной фермы с двухъярусными
шпренгелями необходимо построить л.в. усилия в стойке
основной фермы при движении груза поверху и понизу; способ построения обоих
вариантов л.в. одинаков, разница будет связана только
с разным положением р.р.п., поэтому оба варианта л.в. будут различаться только на участках р.р.п.:
а)
груз Р=1
слева от р.р.п. -
рассматриваем правую часть:
Σ=0; - RB∙9 - S1-2∙4,5 =0; S1-2=
-2∙RB;
л.в.S1-2 = (л.в.RB)∙(-2);
б)
груз Р=1
справа от р.р.п. -
рассматриваем левую часть фермы:
Σ=0; - RA∙3 + S1-2∙4,5 =0; S1-2=
0,667∙RA;
в)
на участках р.р.п. для обоих вариантов проводим свои соединительные прямые;
г)
выполняем анализ передачи груза при различных его положениях на участке
раздвоения л.в.:
– при
положении груза в узлах 7 и 3 он воспринимается шпренгелями, которые передают
его на нижний пояс, поэтому действительной будет ветвь линии влияния для
движения груза понизу;
– при
положении груза в узле 2 шпренгеля не работают и груз
остается на верхнем поясе – ветвь л.в. для движения
груза поверху.
Линия
влияния S3-5 - ? (способ вырезания узла – узел 3):
а)
груз Р = 1 в
узле 3 – ΣZ=0; (аналогично как при
расчете усилия); S3-5= -1;
б)
груз Р = 1 вне узла и вне рассеченных панелей
– ΣZ=0; S3-5= 0;
в)
на участках рассеченных панелей 2-3 и 3-4 проводим переходные
прямые.
3. Усилия от заданной внешней нагрузки по
линиям влияния этих усилий определяем по известной формуле:
S2-3 = S3-4 = 4∙0,79 + 12∙(-0,395) + 4∙0,5∙(-0,79
– 0,263)∙3 + 26∙(-0,132) + 4∙(0,5∙0,263∙1,5) =
-10,54 кН;
S1-5 = 4∙[0,5∙(0,625 - 0,521)∙0,75
- 0,5∙(0,521 +0,208)∙2,25] + 4∙(-0,625) + 12∙0,313 +26∙(-0,104)
+ 4∙(0,5∙0,208∙1,5) = -3,95 кН;
S1-6 = 4∙[0,5∙(0,375 + 0,938)∙0,75
+ 0,5∙(0,938 + 0,375)∙2,25] + 4∙(-0,375) + 12∙0,188 +26∙0,188
+ 4∙(-0,5∙0,378∙1,5) = 12,38 кН;
S1-2 = 4∙[0,5∙(0,417 - 0,5)∙0,75
+ 0,5∙(0,417 + 0,167)∙2,25] + 4∙0,5 + 12∙0,25 + 26∙0,0833
+ 4∙(-0,5∙0,167∙1,5) = 9,167 кН;
S3-5 = 4∙(-0,5∙1∙1,5) = -3 кН;
S5-4 = 4∙[0,5∙(0,625
- 0,416)∙1,5 + 0,5∙(0,416 + 0,208)∙1,5] + 4∙(-0,625) + 12∙0,313
+ 26∙(-0,104) + 4∙(0,5∙0,208∙1,5) = -2,08 кН.
Все
усилия, вычисленные по линиям влияния, совпадают с полученными
из аналитического расчета фермы.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Детали машин Теория машин и механизмов
