Главная
7. Расчет плоских ферм
7.1. Классификация ферм
Фермой называется стержневая система (рис.7.1), остающаяся геометрически неизменяемой после условной замены ее жестких узлов шарнирными.

Рис. 7.1
Иногда используются пространственные фермы, расчет которых обычно сводится к расчету нескольких плоских ферм.
Расстояние между осями опор фермы называется
ее пролетом. Стержни,
расположенные по внешнему контуру, называются поясными и образуют пояса. Вертикальные стержни, соединяющие
пояса, называются стойками,
наклонные – раскосами. Стойки
и раскосы образуют решетку фермы.
Расстояние между соседними узлами пояса фермы называется панелью.
Классификацию ферм обычно проводят по пяти признакам:
1) характеру очертания внешнего контура;
2) типу решетки;
3) типу опирания фермы;
4) назначению;
5) уровню езды.
По характеру очертания различают фермы с параллельными поясами (рис.7.2, а), треугольные фермы (рис.7.2, б) и с ломанным, или полигональным расположением поясов (рис.7.2, в).
а)
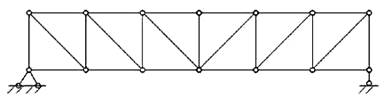
б)

в)
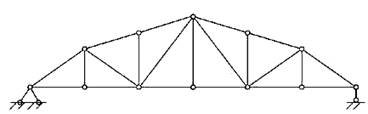
Рис.
7.2
В зависимости от типа решетки различают фермы различных типов. Наиболее распространенными являются раскосные фермы (рис.7.3), фермы с треугольной решеткой (рис. 7.4), фермы с полураскосной решеткой (рис. 7.5) и фермы с ромбической решеткой (рис. 7.6). Раскосы, идущие вверх от опор к середине фермы, называют восходящими раскосами (рис.7.1), идущие наоборот - нисходящими раскосами (рис.7.3). Фермы, усиленные дополнительными стержнями (шпренгелями), называют шпренгельными фермами (рис.7.7).
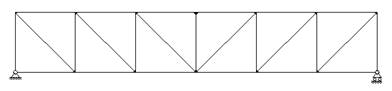
Рис. 7.3

Рис. 7.4
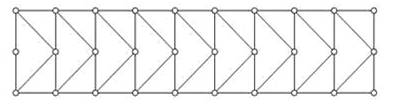
Рис. 7.5
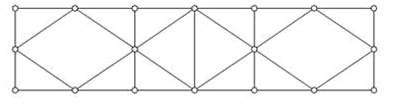
Рис. 7.6

Рис. 7.7
Фермы, как правило, проектируют таким образом, чтобы основная нагрузка на них передавалась через узлы верхнего или нижнего пояса. Наличие шпренгелей позволяет увеличить количество узлов в этом поясе, что может потребоваться для облегчения конструкций, с помощью которых внешняя нагрузка передается на узлы фермы или, например, для уменьшения ширины плит перекрытий, опирающихся на стропильные фермы здания. (рис.7.8).
В зависимости от характера опорных закреплений различают балочные фермы (рис.7.9), консольные фермы (рис.7.10), консольно-балочные фермы (рис.7.11) и арочные фермы (рис.7.12, а,б,в). Кроме того, отдельно рассматриваются различные висячие системы (рис.7.13) и комбинированные системы (рис.7.14).

Рис. 7.8

Рис. 7.9
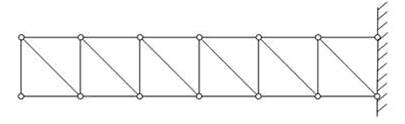
Рис. 7.10
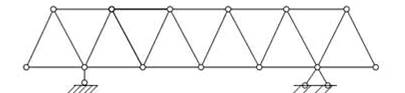
Рис. 7.11
а) 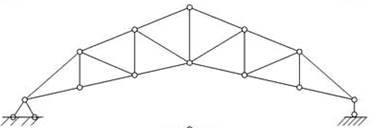
б) 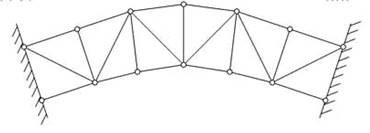
в) 
Рис. 7.12
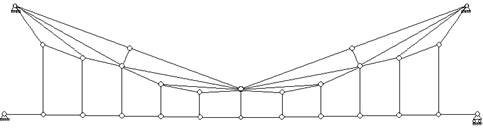
Рис. 7.13

Рис. 7.14
В зависимости от назначения различают фермы стропильные, крановые, башенные, мостовые.
Мостовые фермы в зависимости от уровня езды делятся на фермы с ездой понизу, с ездой поверху и с ездой посередине.
7.2. Статическая работа ферм
Фермы часто используются для перекрытия пролетов, т.е. имеют такое же назначение, что и балки сплошного сечения.
Известно, что при изгибе балки нормальные напряжения в ее поперечных сечениях достигают максимальных значений в верхних и нижних точках сечения. Желание использовать материал балки наиболее экономичным образом заставляет сосредотачивать большую часть материала в наиболее напряженных зонах, что достигается применением балок двутаврового поперечного сечения (рис.7.15). При увеличении пролета и нагрузок высоту балки приходится увеличивать. Следовательно, количество материала в стенке, где напряжения малы, будет расти. Это приведет не только к перерасходу материала в малозагруженной зоне, но и значительно увеличит собственный вес конструкции. Поэтому для экономии материала и облегчения конструкции в вертикальной стенке устраивают вырезы (рис.7.16). С дальнейшим ростом пролета и нагрузок высота сечения конструкции еще увеличивается, и стенка двутавра постепенно переходит в систему стоек. Для того, чтобы полученная конструкция сохраняла геометрическую неизменяемость, т.е. не “сложилась” при действии горизонтальных нагрузок, к системе стоек добавляют систему раскосов, в результате чего и образуется решетка фермы (рис.7.17).



Рис. 7.15 Рис. 7.16
Рис. 7.17
Таким образом, фермы могут быть использованы для перекрытия больших пролетов при действии высоких нагрузок, когда использование балок сплошного сечения оказывается невыгодным или невозможным.
Как и при изгибе балки на двух опорах под действием нагрузки, направленной вниз, стержни верхнего пояса балочной фермы будут сжатыми, а нижнего - растянутыми. В консольной ферме (рис.7.10) ситуация будет обратной.
Узлы фермы, как правило, конструктивно выполняются жесткими. Однако, как показал опыт расчетов, напряжения в стержнях ферм, определенные с учетом жесткости узлов, и напряжения, определенные по шарнирной схеме, обычно отличаются не более, чем на несколько процентов. Поскольку выполнять расчет во втором случае значительно легче, жесткостью узлов фермы пренебрегают и расчет ведут по шарнирной схеме. Иными словами, при расчете фермы все ее узлы считают идеальными шарнирами.

Рис. 7.18
Если все нагрузки на ферму приложены исключительно к узлам, а стержни ферм являются прямыми, то в стержнях ферм действуют только продольные усилия, а изгибающие моменты и перерезывающие усилия отсутствуют. Действительно, вырежем мысленно любой стержень из фермы, заменив действие остальных стержней на него усилиями, передаваемыми через шарниры (рис.7.18). Поскольку других нагрузок на стержень нет, равнодействующие этих сил должны быть направлены по оси стержня. Если бы это было не так, стержень не мог бы находиться в равновесии, в чем легко убедиться, составив уравнение моментов относительно любого из шарниров. Очевидно, единственным усилием, которое в этом случае будет возникать в стержне, будет постоянное по его длине продольное усилие.
7.3. Геометрическая неизменяемость ферм
Для обеспечения геометрической неизменяемости необходимо, во-первых, чтобы связей, наложенных на перемещение узлов фермы было достаточно, во-вторых, они были правильно размещены. Следовательно, исследование геометрической неизменяемости фермы состоит из двух шагов: проверки достаточности числа связей и анализе правильности их размещения (структурном анализе фермы).
Как обычно, при анализе геометрической неизменяемости смещения, вызванные деформированием стержней в расчет не берутся. Иными словами, при анализе геометрической неизменяемости ферм, как и любых других стержневых систем, будем считать стержни абсолютно жесткими.
Каждый узел плоской фермы имеет две степени свободы, т.е. имеет возможность линейного смещения, например, в вертикальном и горизонтальном направлениях. Следовательно, минимальное количество связей, необходимых для закрепления узлов фермы от смещений, должно равняться удвоенному числу узлов. Часть из этих связей должна обеспечивать закрепление фермы относительно основания. Таким образом, минимальное число стержней в ферме, необходимое для обеспечения ее геометрической неизменяемости определяется по формуле:
![]()
где nст - число стержней в ферме, nузл - число узлов, а nоп.св - число опорных связей.
Условие (1) одновременно является условием статической определимости фермы. Действительно, для каждого узла можно составить два уравнения равновесия- условия равенства нулю проекций на вертикальную и горизонтальную оси всех действующих на узел внешних сил и сил, действующих со стороны стержней и реакций опор. Неизвестными же являются продольные усилия в каждом стержне и реакции в опорах. Записав все эти 2∙nузл уравнений, получим систему уравнений, которую в матричной форме можно записать в виде:
AX=B, (2)
где Х - вектор неизвестных усилий в стержнях и опорных связях, В - вектор проекций внешних нагрузок на узлы, А - матрица системы.
Для того, чтобы система (2) была замкнутой, необходимо чтобы число уравнений 2∙nузл совпадало с числом неизвестных, т.е. выполнялось условие (1).
Если количество стержней в ферме будет больше, чем требуется согласно (1), то ферма будет статически неопределимой, если меньше - то геометрически изменяемой.
При этом, важно отметить, что условие (1) является необходимым, но не достаточным для обеспечения геометрической неизменяемости. Как уже упоминалось, кроме обеспечения необходимого числа связей, требуется их правильное размещение.
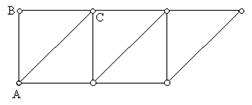
Рис. 7.19
Систему, в которой невозможны взаимные смещения узлов, в предположении, что все стержни абсолютно жесткие, называют жестким диском. В шарнирном треугольнике (например, ABC на рис.7.19) взаимное смещение узлов будет невозможным, следовательно он является жестким диском. Присоединение к такому треугольнику еще одного узла двумя не лежащими на одной прямой связями приведет к образованию системы, в которой также взаимные смещения узлов будут невозможны. Если продолжить этот процесс, то полученная система также будет жестким диском. Примером жесткого диска является простейшая ферма, т.е. ферма, состоящая из шарнирных треугольников (рис.7.19). Взаимные смещения узлов в такой фермы невозможны. Остается только позаботиться о прикреплении полученной простейшей фермы к основанию.
Для того, чтобы обеспечить неподвижность простейшей фермы относительно основания, необходимы как минимум три опорных связи, линии действия которых не параллельны и не пересекаются в одной точке.
Рассмотрим в качестве примера ферму, изображенную на рис.7.1. Очевидно, она относится к простейшим фермам. В ней nст =25, nузл =14, nоп.св =3. Равенство (1) выполняется: 25=2∙14-3=25. Линии действия трех опорных связей (опорных реакций на рис.7.1) не параллельны и не пересекаются в одной точке, следовательно ферма геометрически неизменяема.
Теперь выполним перестановку опорных связей. Отбросим на левой опоре одну связь, сделав неподвижную опору катковой, но добавим еще одну катковую опору в центре пролета фермы (рис.7.20).

Рис. 7.20
В результате, количество опорных связей не изменилось, а осталось равным трем, т.е. равенство (1) осталось справедливым. Однако линии действия опорных связей стали параллельными - направленными вертикально вверх. В результате система получила возможность смещения в горизонтальном направлении, т.е. стала геометрически изменяемой.
Если же в ферме, изображенной на рис.7.1, выполнить перестановку стержней, как показано на рис.7.21, равенство (1) останется неизменным, но система окажется геометрически изменяемой за счет неправильного распределения связей. Это очевидно, т.к. шарнирами C, D, E и F образуется шарнирный квадрат, который при приложении малейшей нагрузки обращается в ромб.
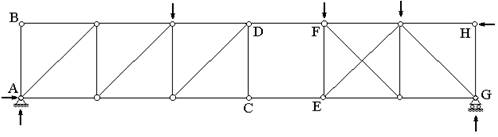
Рис. 7.21
Если ферма образована из двух жестких дисков, то для того, чтобы исключить взаимные смещения узлов в полученной системе, необходимо, чтобы они соединялись между собой как минимум тремя связями, линии действия которых не параллельны и не пересекаются в одной точке.
В ферме на рис.7.21 два жестких диска ABCD (он представляет собой простейшую ферму) и FEGH (ферма, образованная из простейшей добавлением одной “лишней” связи) соединяются между собой только двумя связями DF и CE, что и приводит к геометрической изменяемости фермы, в чем мы уже убедились.
Рассмотрим арочную ферму, изображенную на рис.7.12,в. Здесь nст =18, nузл =11, nоп.св =4. Условие (1) выполняется: 18=11∙2-4=18. Эта ферма также образована двумя жесткими дисками (простейшими фермами). Они соединяются между собой шарниром С, т.е., на первый взгляд, только двумя связями, т.к. шарнир препятствует взаимному смещению соединяемых им узлов в вертикальном и горизонтальном направлениях. Однако, поскольку опоры А и В неподвижны, взаимных горизонтальных смещений точек А и В быть не может. Значит, роль третьей связи играет основание. Поэтому рассматриваемая система геометрически неизменяема, а в обеих опорах возникнут горизонтальные распорные реакции.
Выполним перестановку связей в этой ферме. Сделаем одну из опор катковой, сняв таким образом ограничение на взаимные горизонтальные смещения точек А и В. Однако, добавим стержень, который возьмет на себя роль третьей связи, соединяющей простейшие фермы (рис.7.22). Равенство (1) при этом не нарушится: 19=11∙2-3=19, система останется геометрически неизменяемой, а роль основания по восприятию горизонтального усилия перейдет введенному стержню, работающему в качестве затяжки.

Рис. 7.22
В качестве еще одного примера рассмотрим ферму Шухова (рис.7.23). В ней nст =9, nузл =6, nоп.св =3. Условие (1) выполняется: 9=6∙2-3=9.

Рис. 7.23
Ферма образована двумя шарнирными треугольниками ABC и DEF, связанными между собой тремя связями- AF, BE, и DC, линии действия которых не параллельны и не пересекаются в одной точке. Прикрепление образованного в результате жесткого диска к основанию выполнено при помощи одной неподвижной и одной катковой опоры, т.е. также при помощи трех связей, линии действия которых не параллельны и не пересекаются в одной точке. Следовательно, ферма геометрически неизменяема.
В случаях, когда простым структурным анализом не удается доказать геометрическую неизменяемость фермы, приходится пользоваться более сложными методами. Одним из них является статический метод анализа геометрической неизменяемости ферм. Идея метода заключается в следующем. Для геометрически изменяемой фермы система уравнений (2) не должна иметь решений, следовательно матрица А должна быть особенной, т.е. ее определитель должен быть равен нулю. Как известно, если в однородной системе линейных алгебраических уравнений АХ=0 определитель матрицы А равен нулю, то система кроме тривиального решения Х=0 допускает и ненулевое решение. Поэтому, в стержнях статически определимой, но геометрически изменяемой фермы при нулевой нагрузке может возникнуть система самоуравновешенных сил.
Для того, чтобы доказать геометрическую неизменяемость фермы, необходимо доказать, что при отсутствии внешней нагрузки в ее стержнях не может возникнуть усилий. Если же оказывается, что при отсутствии нагрузки в стержнях фермы могут существовать ненулевые усилия, то это указывает на равенство определителя матрицы А нулю, а значит и на геометрическую изменяемость фермы.
При выполнении анализа подобного рода, как и при выполнении статического расчета фермы, оказываются полезными правила определения нулевых стержней. Нулевым стержнем называется стержень, в котором при рассматриваемой нагрузке усилие равно нулю. Приведем эти правила.
1. Если в незагруженном узле под углом соединяются два стержня, то оба стержня - нулевые (рис.7.24). В этом легко убедиться, составив уравнения проекций сил на оси, совпадающие с направлением стержней.
2. Если в незагруженном узле сходятся сходятся три стержня, причем два лежат на одной прямой, то третий стержень - нулевой (рис.7.25). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную двум стержням, лежащим на одной прямой.
3. Если к узлу, в котором сходятся два стержня, приложена сила, направление действия которой совпадает с одним из них, то второй стержень - нулевой (рис.7.26). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную линии действия внешней силы.



Рис. 7.24 Рис. 7.25 Рис. 7.26
4. Если в узле сходятся три и более стержней, то те из них, о которых заранее известно, что они являются нулевыми, при определении остальных нулевых стержней и нахождении усилий в стержнях, очевидно, могут быть мысленно отброшены.
5. Если обо всех стержнях кроме одного, сходящихся в незагруженном узле, известно, что они нулевые, то и последний стержень тоже будет нулевым. В этом легко убедиться, составив уравнение проекций сил на ось, совпадающую с направлением этого стержня.
Рассмотрим в качестве примера ферму, изображенную на рис.7.27.
Для нее nст =22, nузл =15, nоп.св =8. Условие (1) выполняется: 22=15∙2-8=22. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т.е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отсутствии внешней нагрузки.

Рис. 7.27
Из рассмотрения узлов 5 и 7, согласно признаку 2 нулевых стержней следует, что стержени 3-5 и 7-6 - нулевые. Далее, из рассмотрения узла 3, согласно признакам 4 и 2 следует, что стержень 2-3 нулевой. Далее, из рассмотрения узла 2, согласно признакам 4 и 1 следует, что стержни 1-2 и 2-6 - нулевые. Далее, из рассмотрения узла 6, согласно признакам 4 и 2 следует, что стержень 3-6 нулевой, а значит, в соответствии с признаком 5, нулевым будет и стержень 6-8. Далее, из рассмотрения узла 3, согласно признаку 5 следует, что стержень 1-3 нулевой. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно стержни 8-10, 10-14, 14-15, 9-10, 11-12, 12-14, 10-12 и 12-15 тоже будут нулевыми. Рассмотрим теперь узел 8. В соответствии с признаками 4 и 1 стержень 7-8 будет нулевым. Далее, последовательно рассматривая узлы 7 и 5, пользуясь признаком 5, докажем, что стержни 5-7 и 4-5 - нулевые. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно 8-9, 9-11, 11-13, тоже будут нулевыми. Итак, нам удалось доказать, что все стержни фермы при отсутствии нагрузки являются нулевыми. Следовательно, в этом случае в них не может возникнуть ненулевые усилия, а значит ферма геометрически неизменяема.
Теперь рассмотрим ферму, изображенную на рис.7.28.

Рис. 7.28
Для нее nст =10, nузл =7, nоп.св =4. Условие (1) выполняется: 10=7∙2-4=10. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т.е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отсутствии внешней нагрузки.
Рассмотрим узел 1. Поскольку на него может действовать только вертикальная опорная реакция, в соответствии с признаком 3 нулевых стержней стержень 1-3 является нулевым. Из рассмотрения узла 7 тот же вывод можно сделать о стержне 5-7. Рассмотрим далее узел 3. На основании признаков 2 и 4 нулевых стержней можно заключить, что стержень 3-5 нулевой.
Предположим, что в стержне 1-2 возникло растягивающее усилие N1-2=N. Рассмотрим равновесие узла 2 (рис.7.29). Составим для него уравнения проекций действующих на узел усилий на вертикальную и горизонтальную оси: N2-3cos𝛼=N, N2-6=N2-3sinα, откуда следует, что N2-3=N/cos𝛼, а N2-6=N∙tg𝛼. Рассмотрим далее равновесие узла 6 (рис.7.30). Из аналогичных уравнений равновесия, составленных для этого узла, получим: N2-6=N6-5∙sinα, N6-5∙cosα=N6-7.
Отсюда следует, что
![]()
Рассмотрим далее равновесие опорных узлов. Учитывая отсутствие усилий в стержнях 1-3, 3-5 и 3-7, из рассмотрения равновесия узлов 3 и 5 (из уравнения проекций сил на оси, совпадающие с направлением стержней 2-3 и 6-5) легко заключить, что N2-3 =N3-4 и N6-5 =N4-5. Из уравнения равновесия проекций сил на вертикальную ось для узла 4 (рис.7.31), получим: N3-4∙cosα+N4-5∙cosα=V4, где V4 - вертикальная опорная реакция.
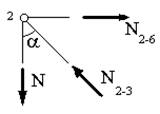


Рис. 7.29 Рис.
7.30 Рис. 7.31
Отсюда следует, что
![]()
Легко убедиться, что в каждой их двух других опор действует вертикальная реакция величиной N, направленная вверх. Составим для фермы уравнение проекций всех сил на вертикальную ось. Поскольку внешняя нагрузка отсутствует, в него будут входить только опорные реакции. Очевидно, их равнодействующая равна нулю, а значит система находится в равновесии.
Таким образом, мы доказали, что в стержнях фермы при отсутствии внешней нагрузки может иметься система самоуравновешенных сил, что говорит о том, что ферма геометрически изменяема.
Если бы в процессе подобных рассуждений мы столкнулись с противоречием (например, невозможностью удовлетворить уравнениям равновесия) или доказали бы, что все стержни фермы - нулевые, то отсюда следовала бы невозможность существования такой системы усилий, а значит ферма была бы геометрически неизменяемой.
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

