Главная
9.16.3.
Алгоритм МКЭ для динамической задачи
При анализе динамического поведения биологических структур, требуемого в ряде задач биомеханики, как правило, необходимо учитывать вязкость живых тканей. В теории наследственной упругости и в работах, посвященных моделированию мягких тканей, известно большое число определяющих соотношений вязко-упругого материала, задающих связь между скоростями деформаций и напряжений. В настоящем курсе мы рассмотрим наиболее известную модель такого материала, носящую название модель Кельвина-Фойгта и описываемую следующим тензорным соотношением (9.217):
Приведенное выражение позволяет достаточно легко расширить рассмотренный выше алгоритм на решение динамических задач с учетом вязкости материала. В частности, модель Кельвина-Фойгта удобна для анализа отклика биомеханической системы на приложенное гармоническое воздействие. В одной из следующих лекциях будет продемонстрирован пример применения данной модели к решению некоторых актуальных задач биомеханики опорно-двигательного аппарата человека.
Перепишем определяющее соотношение модели Кельвина-Фойгта в матричной форме, введя в рассмотрение наряду с матрицей упругих модулей D еще и матрицу вязкости S:
С учетом нового выражения для вектора напряжений вычислим вариацию потенциальной энергии деформации тела:
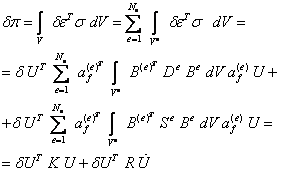
где
-
элементная матрица диссипации
- глобальная
матрица диссипации
Вектор сил инерции может быть выражен через глобальный вектор узловых ускорений путем применения процедуры конечно-элементной дискретизации, описанной выше:
Элементарная работа внешних объемных сил должна быть преобразована с учетом сил инерции, действующих на точки тела. Согласно принципу Даламбера силы инерции могут быть добавлены к активным внешним силам, что в результате приводит к следующему выражению виртуальной работы объемных сил:
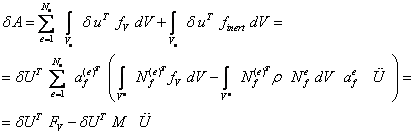
где
- элементная
матрица масс
- глобальная
матрица масс
Наконец, применяя основное математическое выражение принципа возможных перемещений:
,
с учетом нового вида виртуальной работы и вариации потенциальной энергии деформации, получим следующее обыкновенное дифференциальное уравнение относительно глобального вектора узловых перемещений в матричном виде:
, (9.222)
где U(t) - глобальный вектор узловых перемещений, зависящих от времени,
F(t)= Fv(t)+Fs(t) - глобальный вектор узловых сил, зависящих от времени.
Полученное дифференциальное уравнение широко используется в методе конечных элементов для решения динамических задач. В данной главе мы рассмотрим только частный случай общей динамической задачи - вынужденные колебания тела под действием внешней гармонической силы. Несмотря на частный характер, теоретический анализ вынужденных колебаний биомеханических структур актуален при решении важных практических задач, связанных с разработкой вибрационных методов исследования состояния живых тканей и органов, что будет показано в дальнейшем.
9.16.4.
Расчет вязко-упругих гармонических колебаний
Для разработки алгоритма воспользуемся известным подходом, применяемым в теории линейных колебаний. Представим внешнюю гармоническую силу в виде комплексной экспоненты:
,
где F, 
- глобальный вектор амплитудных
значений узловых сил и круговая частота колебаний силы, i -
мнимая единица.
Тогда частное решение, соответствующее установившемся вынужденным колебаниям ищется в том же виде, что и правая часть дифференциального уравнения:
,
где U - глобальный вектор комплексных амплитудных значений узловых перемещений; U1 and U2 - соответственно действительная и мнимая части данного вектора.
Подставляя выражения сил и перемещений в дифференциальное уравнение, получим систему комплексных алгебраических уравнений относительно глобального вектора комплексных амплитуд:
(9.223)
После решения полученной системы для фиксированных значений частоты внешней силы, действительные амплитудные значения перемещений узлов, их скоростей и ускорений могут быть вычислены следующим образом:
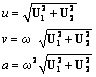
email: KarimovI@rambler.ru Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
